Scheme of Work

Mathematics Scheme of Work for SS1-3 Senior Sec School in Nigeria all Term

Posted by

Many Secondary School Teacher and Parent whose child or children are about to get their education in Nigeria are looking for how to download Mathematics Scheme of Work SOW for Senior Secondary School in Nigeria SS1, SS2, SS3; First, Second and Third Term for WAEC or NECO.

If you are here, then you are at the right page

What Others are downloading
Mathematics Scheme of Work
Mathematics SS1-3 Exam Questions
Mathematics SSCE Past Questions and Answers – WAEC, NECO, NABTEB
Lesson Note

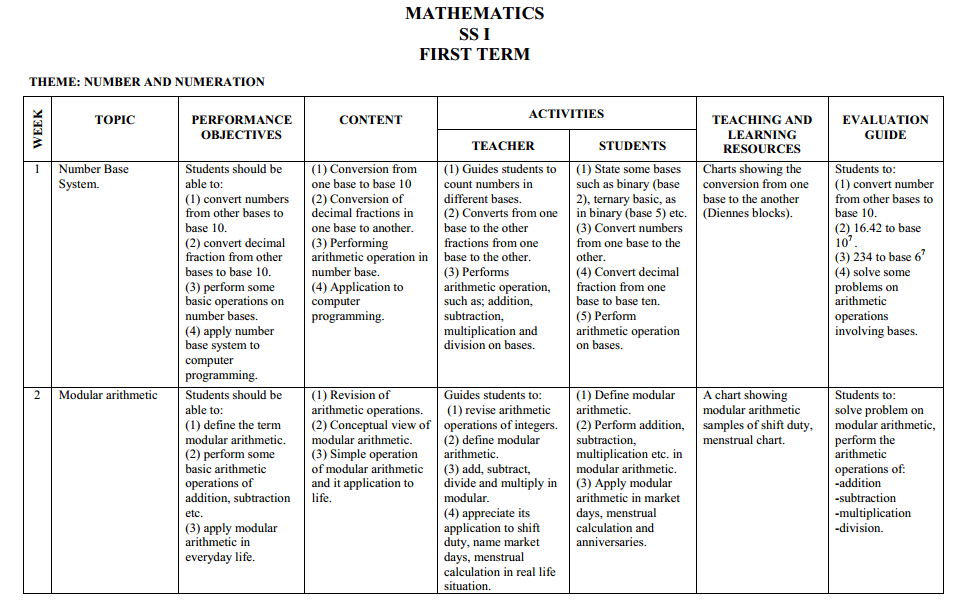
mathematics scheme of work ss1-3 in Nigeria

Mathematics Scheme of Work for SS1 in Nigeria

Topic Outline for SS1 First Term

THEME: NUMBER AND NUMERATION
Number Base System.
Modular arithmetic
Indices
Logarithms
Effective use of logarithm tables in calculations

THEME: ALGEBRAIC PROCESSES
Simple Equations and variations
Quadratic Equation
Formation of quadratic equations with given roots.
Logical Reasoning
Logical operations and their symbols
Revision
Examination.

SS2 Mathematics Scheme of Work 2nd Term

Topic Outline for SS2 Second Term

Logical Reasoning
Logical Reasoning
Linear Inequalities
Linear Inequalities
Algebraic Fractions
Algebraic Fractions

THEME: GEOMETRY
Chord Property
Chord Property
Circle Theorems
Circle Theorems
Revision
Examination.

Maths Scheme of Work for SS3 First Term

Topic Outline for SS3 First Term

THEME: NUMBER AND NUMERATION
Surds
Matrices and determinants
Matrices and determinant (continued)
Logarithms and indices.
Arithmetic of finance
Arithmetic of finance (continued)

THEME: ALGEBRAIC PROCESSES
Application or linear and quadratic equations to capital market

THEME: GEOMETRY
Trigonometry: Graphs of trigonometric ratios.
Trigonometry of graphs of sine, cosine and tangent.
Surface Area
Revision of Team Work
Examination

Mathematics Scheme of Work for Senior Secondary School in Nigeria

Here is a sample of SS3 Mathematics (Week 1 -10) First Term Complete Scheme of Work SOW in tabular format that entail Weekly Topic Outline/Content; Teacher and Student Activities

WEEKTOPICCONTENTTEACHER ACTIVITIESSTUDENT ACTIVITIES
1surd(1) Meaning of rational and irrational numbers reading to the definition of surds
(2) The rules guiding the basic operation with surds i.e.
(3) Conjugate of a binomial surds using the idea of difference of two squares.
(4) Application to solving triangles involving trigonometric ratios of special angles of 30o , 60o and 45o
(5) Evaluation of expression involving surds.		Guides students to: (1) Differentiate between the rational and irrational numbers leading to the definition of surds.
(2) Perform the operation of addition and subtraction of numbers in surdic form.
(3) Conjugate binomial surds using the idea leading to the difference of two squares.
(4) Appreciate the application of surds to trigonometric rations e.g.		(1) Differentiate between rational and irrational number leading to the definition of surds.
(2) Perform and solve problems on addition, subtraction, multiplication and division of surdic numbers.
(3) Verify the rules of the operation of addition, subtraction, multiplication and division.
(4) Apply the principle of difference of two squares to conjugate surdic expressions.
(5) Relate surds to trigonometric ratio.
2Matrices and determinants(1) Definition order and notation of matrix.
(2) Types of matrices e.g. addition and subtraction of matrices,
(3) Scalar multiplication of matrices and multiplication of matrices/general matrix multiplication.		Leads students to:
(1) Defines matrix
(2) State the order and notation of matrices.
(3) Identifies and define different types of matrices. (4) Performs the operation of addition, subtraction of matrices.
(5) Multiplies matrix by a scalar.		(1) Define matrix
(2) Identify matrix notations.
(3) Identify different types of matrices.
(4) Perform and solve problems on addition and subtraction of matrices.
3Matrices and determinant (continued)(1) Determinants of 2×2 and 3×3 matrices.
(2) Transpose of a matrix
(3) Matrices and simultaneous equations.		(1) Performs the multiplication by a quantity as well as matrix-matrices multiplication
(2) Finds the transpose of a matrix by interchanging the rows and columns.
(3) Calculates the determinants of matrices.
(4) Appreciates the application of matrices to solutions of simultaneous equations.		(1) Perform multiplication by a scalar quantity and matrix by matrix multiplication.
(2) Find the transpose of a given matrix by interchanging row with column
(3) Calculate determinants of matrices
(4) Apply matrix operations to real life situations including solving simultaneous equations.
4Logarithms and indices.(1) Revision of laws of indices and laws of logarithm.
(2) Use laws of logarithm to simplify and/or evaluate given expressions without the use of logarithm table.
(3) Use logarithm table for purpose of calculation.		(1) Brings to the class charts of logarithm and solution from the prepared charts.
(2) Guides students to deduce logarithm laws.
(3) Uses the deduced logarithm and logarithm table to calculate problems.		(1) Study the two charts.
(2) Deduce laws of logarithm especially
(3) Verify logarithm laws with simple exercises.
(4) Revise use of logarithm table to solve problems involving calculation
5Arithmetic of finance(1) Simple interest (Revision)
(2) compound interest
(3) Depreciation
(4) Annuities (5) Amortization		Guides students to:
(1) recall the formula for simple interest.
(2) drive formula for computing compound interest.
(3) compute depreciation value of an item
(4) determine the annuities
(5) compute the amortization		(1) Use formula to calculate simple interest, compound interest.
(2) Compute depreciation value of a given item
(3) Compute the annuity paid on a sum of money at regular interval.
(4) Compute the amortization
6Arithmetic of finance continueFurther use of logarithm table in problem involving: (1) Bonds and debenture (2) Shares
(3) Rates
(4) Income tax
(5) Value added tax		(1) Shows the solution chart.
(2) Calculates interest on bound and debenture purchase either by individual or institution e.g. value added tax on the floor of the exchange market attracts 0.5% of the price.
(3) Carries simple calculation involving rates, taxes, value added tax (VAT)		(1) Study the solution charts of logarithm in calculating interest in bond and debenture.
(2) Calculate interest on bond and debenture purchase by an individual or institution using logarithm table.
(3) Solve problems on rates, taxes and value added tax.
7Application or linear and quadratic equations to capital market.(1) Revision of solution of simultaneous linear and quadratic equation
(2) Word problems on linear equations, simultaneous linear equations, quadratic equations are linear are quadratic.
(3) Application to capital market.		(1) Displays chart of simple linear and quadratic equation. (2) Revises the solution of simultaneous linear and quadratic equations.
(3) Guides students to discover how word problems can be interpreted into linear, quadratic and simultaneous equations.
(4) Solves problems in linear equations such as (i) a father and his son are share holders in a public liability company. The father invests 3 times as much as the son. If they invest altogether amount to 3000 shares of N50, 000 per share etc. How did the father invest?		(1) Study the chart
(2) Solve the solution of simultaneous linear and quadratic equation.
(3) Use steps given by the teacher to solve word problems
(4) Solve problems involving on linear, one quadratic equation following teachers guide and suggestion.
8Trigonometry: Graphs of trigonometric ratios.(1) Construct tables of values for sine and cosine graphs
(2) Plot graphs of sine and cosine for 0 <  x <  360 o 		Guides students to:
(1) Constructs table of values 0 <   x <  360 o for sine and cosine graphs.
(2) Plots graphs of sine and cosine for   0 <  x <  360 o
(3) On chalkboard
(4) Interprets the graphs of sine and cosine and read out given values.		(1) Construct table of values.
(2) Plot graphs of tables of values on their graph books.
(3) Interpret the graphs of sine and cosine and read out given values
9.Trigonometry of graphs of sine, cosine and tangent.(1) Graphs of sine, cosine and tangent for 0 £   x £  360o(2) Graphical solution of simultaneous linear and trigonometric equation.(1) Separates equation containing linear expression and trigonometric ratios
(2) Prepares table of values of both linear and trigonometric ratio.
(3) Plots the sine type of graphs on the page.
(4) Read values from graphs.
10.Surface AreaSurface area of a sphere and hemisphere.(1) Brings a sphere to the classroom
(2) Explains the concept of the surface area.
(3) Leads students to find the surface area of a sphere with given dimension		(1) Study the sphere and state its characteristics
(2) Note the concepts of surface area.
(3) Find the surface area of a sphere
(4) Solve problems on surface area of a sphere.
11REVISION OF TEAM WORK   
12EXAMINATION   

Download Maths Scheme of Work for WAEC or NECO

Click to download your Complete SS3 First Term Mathematics Scheme of Work in PDF Week 1-10

Download Link 1 SOW for Mathematics Link 2: SOW for Mathematics

How to get Complete Mathematics Scheme of Work SS1-3.

To get the complete Mathematics Scheme of work for senior secondary school that entails the following.
All three Term, Week 1-10, Topic Content, Performance Objective, Activities, Teaching and Learning Resource/Materials, Evaluation and Guide

Take Note of the following step

Take Action
Call or whatsapp us on 08051311885 for the account number to make payment and how to received your complete copy of the SOW to be sent directly to your email address or whatsapp number.

Mode of Payment.
Mobile Transfer, POS or Direct Bank Deposit

After Payment
send us the following
Depositor Name:
Name of Product Paid for:
Valid email address.

Mode of Delivery
After payment, it will be sent to your email address or whatsapp

Please Take Note:
The scheme of work is in PDF soft copy format.
It can be view and read using a smart mobile phone or personal computer (pc)
It can be printed out into hard copy.
It is not free (do not chat me up if your intention is to beg for it)
It cost a token.

Other Available Products
Lesson Note and Exam Questions for Primary to Senior Secondary School

Related Posts:

  1. English Language Scheme of Work for JSS 1-3 1st, 2nd, 3rd Term Download PDF
  2. History Scheme of Work for Secondary School in Nigeria Junior and Senior
  3. Mathematics Scheme of Work for JSS 1, 2, 3 All Term in Nigeria
  4. Civic Education Scheme of Work for SS1, SS2, SS3 All Term
  5. Technical Drawing Scheme of Work for SS1-3 Senior Sec School

Leave a Reply

Your email address will not be published. Required fields are marked *